Niall Murphy

When solving problems with biological computers, it sometimes seems more intuitive to directly encode a problem instance into the computation machinery. For example, many of the first DNA computers directly encoded problem instances into experimental protocols so that a unique protocol was required for each instance of the problem considered. This way of encoding a problem is known as semi-uniformity in contrast to the more general uniformity (e.g.\ Boolean circuits) where there is one device to solve all problem instances of a certain size. Previously most researchers intuitively felt that while uniformity was more desirable than semi-uniformity the two concepts were computationally identical. We show that for a simple class of circuits, uniform families are strictly weaker than semi-uniform ones. This result is applicable to any implementation of family style computing systems (e.g. Boolean circuits, membrane systems, DNA strand displacement etc.).

We introduce tight (more appropriate) uniformity conditions to membrane computing and find that some models are actually exponentially weaker than previously thought.

Some definitions is the world of membrane systems are vague and open to interpretation. In this paper we consider some interpretations of the halting and acceptance conditions. It is surprising that this can result in a change in the computing power of the system. This idea was revisited more throughly in "Uniformity is weaker than semi-uniformity for some membrane systems" above.

We introduce tight (more appropriate) uniformity conditions to membrane computing and find that some models are actually exponentially weaker than previously thought. This idea was revisited more throughly in "The computational power of membrane systems under tight uniformity conditions" above.

In the early 1960's Gilbert Hasenjaeger built several mechanical devices to demonstrate the concept of a Turing machine to his students at the Universities of Münster and Bonn. Using old telephone relays and rotary switches forced him to build a machine that uses remarkably few rules and to simulate a simple non-erasing model, namely Wang's B machines.

B machines have been used to show that a number of other models are universal over the past 60 years. Unfortunately, via previous proofs, these models suffered from an exponential slowdown when simulating Turing machines. We show that Wang's B machines actually simulate Turing machines in polynomial time.

Since Hasenjaeger's machine simulates Wang B machines, it too is an efficient model of computation.

Hasenjaeger's machine is currently on display in the Heinz Nixdorf MuseumsForum, Germany, and a video of the machine in action can be seen here or here.

Membrane systems, or P-systems are a model of computation that abstracts the inner workings of cells. Using this model we can characterise the sets of problems that membrane systems can solve with limited resources. The hope is that as efforts to implement cellular computers progress that the theoretical results from membrane systems will be a guide to synthetic biologists as to how different cellular mechanisms affect the computing power of the resulting cell.

Cell division seems to allow computers implemented in living cells to create an exponential number of self-replicating parallel computing devices. While in the real world, this level of perfect parallelism is impossible, some level of parallelism is often desirable.

The P-Conjecture, stated in 2007 asks what features of membrane computing are essential to take advantage of the exponential growth of membrane systems. In particular it asks: if cells have no way to indicate an internal change of state to the outside world, can the overall system be parallel?

For a system to be parallel we show that it can solve problems in PSPACE in polynomial time, or problems in NC in poly-logarithmic time. To show a system is sequential, that is, that it probably (assuming that NC ≠ P, or P ≠ PSPACE) can never be parallelised, we show that it exactly characterises the complexity class P.

The original statement of the P-Conjecture remains unsolved, but my co-authors and I have made significant progress.

This paper is the closest result to finally resolving the P-Conjecture. We showed that if both daughter cells resulting from a division are identical, that is the division was symmetric, that the system probably cannot solve problems in a parallel way. By storing just a single copy of each archetype membrane and then manipulating counters as the system develops over time we can simulate such a system in a standard computer using polynomial time and memory.

In this paper we consider a system that uses only two rules, cell division and cell dissolution. These rules were key to providing parallelism in other P-conjecture attempts. We showed that with just this combination that the exponential number of membranes can be compressed into a polynomially sized tree and that by following the movement of objects around this tree needs only polynomial time.

In this technical report we find a possible link between the degree of power of division in a system, and the resulting degree of parallelism. We hope that by trying to characterise the Polynomial Hierarchy we would gain insight into the P-Conjecture.

There are theoretical limits on how fast we can sort a list of numbers. However, in their daily activities, physical scientists routinely sort millions of molecules. In fact, the number of molecules being sorted does not affect the time needed. Instead the resolution of the sorted list increases with time.

For example, microbiologists sort millions of DNA molecules by length. 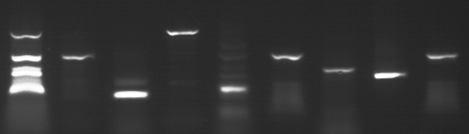(Image supplied by Beverley Henley and Kieran McDermott.)

Similarly, a prism can sort innumerable beams of light according to their wavelength.

Could it be possible to use a special purpose hardware component that we could plug into a standard computer to sort in constant time? We look at several processes: gel electrophoresis, chromatography, optical tweezers, refraction of light, and mass spectrometry. From these we abstract a model of computation that captures a general method of physical sorting. While this model allows us to sort a list in constant time, there is a major bottle neck. For such a device to be useful it must connect with a standard computer, such as a Turing machine or Boolean circuit. Unfortunately, inputting the list to sort or reading off the output makes our super fast sorting device behave just as poorly as a standard sequential algorithm.